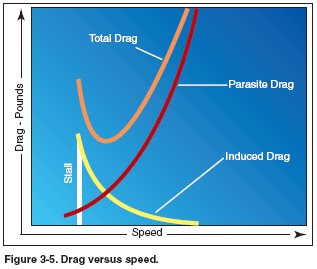
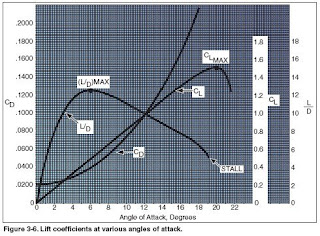
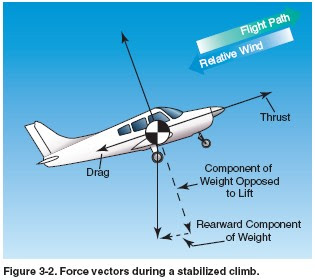
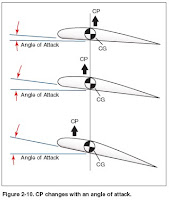
In designing an airplane, a great deal of effort is spent in developing the desired degree of stability around all three axes. But longitudinal stability about the lateral axis is considered to be the most affected by certain variables in various flight conditions.
Longitudinal stability is the quality that makes an airplane stable about its lateral axis. It involves the pitching motion as the airplane’s nose moves up and down in flight. Alongitudinally unstable airplane has a tendency to dive or climb progressively into a very steep dive or climb, or even a stall. Thus, an airplane with longitudinal instability becomes difficult and sometimes dangerous to fly.
Static longitudinal stability or instability in an airplane, is dependent upon three factors:
Location of the wing with respect to the center of gravity;
Location of the horizontal tail surfaces with respect to the center of gravity; and
The area or size of the tail surfaces.
In analyzing stability, it should be recalled that a body that is free to rotate will always turn about its center of gravity.
To obtain static longitudinal stability, the relation of the wing and tail moments must be such that, if the moments are initially balanced and the airplane is suddenly nosed up, the wing moments and tail moments will change so that the sum of their forces will provide an unbalanced but restoring moment which, in turn, will bring the nose down again. Similarly, if the airplane is nosed down, the resulting change in moments will bring the nose back up.
The center of lift, sometimes called the center of pressure, in most unsymmetrical airfoils has a tendency to change its fore and aft position with a change in the angle of attack. The center of pressure tends to move forward with an increase in angle of attack and to move aft with a decrease in angle of attack. This means that when the angle of attack of an airfoil is increased, the center of pressure (lift) by moving forward, tends to lift the leading edge of the wing still more. This tendency gives the wing an inherent quality of instability.
 Figure 3-12 shows an airplane in straight-and-level flight. The line CG-CL-T represents the airplane’s longitudinal axis from the center of gravity (CG) to a point T on the horizontal stabilizer. The center of lift (or center of pressure) is represented by the point CL.
Figure 3-12 shows an airplane in straight-and-level flight. The line CG-CL-T represents the airplane’s longitudinal axis from the center of gravity (CG) to a point T on the horizontal stabilizer. The center of lift (or center of pressure) is represented by the point CL.
Most airplanes are designed so that the wing’s center of lift (CL) is to the rear of the center of gravity. This makes the airplane “nose heavy” and requires that there be a slight downward force on the horizontal stabilizer in order to balance the airplane and keep the nose from continually pitching downward. Compensation for this nose heaviness is provided by setting the horizontal stabilizer at a slight negative angle of attack. The downward force thus produced, holds the tail down, counterbalancing the “heavy” nose. It is as if the line CG-CL-T was a lever with an upward force at CL and two downward forces balancing each other, one a strong force at the CG point and the other, a much lesser force, at point T (downward air pressure on the stabilizer). Applying simple physics principles, it can be seen that if an iron bar were suspended at point CL with a heavy weight hanging on it at the CG, it would take some downward pressure at point T to keep the “lever” in balance.
 Even though the horizontal stabilizer may be level when the airplane is in level flight, there is a downwash of air from the wings. This downwash strikes the top of the stabilizer and produces a downward pressure, which at a certain speed will be just enough to balance the “lever.” The faster the airplane is flying, the greater this downwash and the greater the downward force on the horizontal stabilizer (except “T” tails). [Figure 3-13] In airplanes with fixed position horizontal stabilizers, the airplane manufacturer sets the stabilizer at an angle that will provide the best stability (or balance) during flight at the design cruising speed and power setting. [Figure 3-14]
Even though the horizontal stabilizer may be level when the airplane is in level flight, there is a downwash of air from the wings. This downwash strikes the top of the stabilizer and produces a downward pressure, which at a certain speed will be just enough to balance the “lever.” The faster the airplane is flying, the greater this downwash and the greater the downward force on the horizontal stabilizer (except “T” tails). [Figure 3-13] In airplanes with fixed position horizontal stabilizers, the airplane manufacturer sets the stabilizer at an angle that will provide the best stability (or balance) during flight at the design cruising speed and power setting. [Figure 3-14]
 If the airplane’s speed decreases, the speed of the airflow over the wing is decreased. As a result of this decreased flow of air over the wing, the downwash is reduced, causing a lesser downward force on the horizontal stabilizer. In turn, the characteristic nose heaviness is accentuated, causing the airplane’s nose to pitch down more. This places the airplane in a nose-low attitude, lessening the wing’s angle of attack and drag and allowing the airspeed to increase. As the airplane continues in the nose-low attitude and its speed increases, the downward force on the horizontal stabilizer is once again increased.
If the airplane’s speed decreases, the speed of the airflow over the wing is decreased. As a result of this decreased flow of air over the wing, the downwash is reduced, causing a lesser downward force on the horizontal stabilizer. In turn, the characteristic nose heaviness is accentuated, causing the airplane’s nose to pitch down more. This places the airplane in a nose-low attitude, lessening the wing’s angle of attack and drag and allowing the airspeed to increase. As the airplane continues in the nose-low attitude and its speed increases, the downward force on the horizontal stabilizer is once again increased.
Consequently, the tail is again pushed downward and the nose rises into a climbing attitude.
As this climb continues, the airspeed again decreases, causing the downward force on the tail to decrease until the nose lowers once more. However, because the airplane is dynamically stable, the nose does not lower as far this time as it did before. The airplane will acquire enough speed in this more gradual dive to start it into another climb, but the climb is not so steep as the preceding one.
After several of these diminishing oscillations, in which the nose alternately rises and lowers, the airplane will finally settle down to a speed at which the downward force on the tail exactly counteracts the tendency of the airplane to dive. When this condition is attained, the airplane will once again be in balanced flight and will continue in stabilized flight as long as this attitude and airspeed are not changed.
A similar effect will be noted upon closing the throttle. The downwash of the wings is reduced and the force at T in figure 3-12 is not enough to hold the horizontal stabilizer down. It is as if the force at T on the lever were allowing the force of gravity to pull the nose down. This, of course, is a desirable characteristic because the airplane is inherently trying to regain airspeed and reestablish the proper balance.
 Power or thrust can also have a destabilizing effect in that an increase of power may tend to make the nose rise. The airplane designer can offset this by establishing a “high thrustline” wherein the line of thrust passes above the center of gravity. [Figures 3-15 and 3-16] In this case, as power or thrust is increased a moment is produced to counteract the down load on the tail. On the other hand, a very “low thrust line” would tend to add to the nose-up effect of the horizontal tail surface.
Power or thrust can also have a destabilizing effect in that an increase of power may tend to make the nose rise. The airplane designer can offset this by establishing a “high thrustline” wherein the line of thrust passes above the center of gravity. [Figures 3-15 and 3-16] In this case, as power or thrust is increased a moment is produced to counteract the down load on the tail. On the other hand, a very “low thrust line” would tend to add to the nose-up effect of the horizontal tail surface.
It can be concluded, then, that with the center of gravity forward of the center of lift, and with an aerodynamic tail-down force, the result is that the airplane always tries to return to a safe flying attitude.
 Asimple demonstration of longitudinal stability may be made as follows: Trim the airplane for “hands off” control in level flight. Then momentarily give the controls a slight push to nose the airplane down. If, within a brief period, the nose rises to the original position and then stops, the airplane is statically stable. Ordinarily, the nose will pass the original position (that of level flight) and a series of slow pitching oscillations will follow. If the oscillations gradually cease, the airplane has positive stability; if they continue unevenly, the airplane has neutral stability; if they increase, the airplane is unstable.
Asimple demonstration of longitudinal stability may be made as follows: Trim the airplane for “hands off” control in level flight. Then momentarily give the controls a slight push to nose the airplane down. If, within a brief period, the nose rises to the original position and then stops, the airplane is statically stable. Ordinarily, the nose will pass the original position (that of level flight) and a series of slow pitching oscillations will follow. If the oscillations gradually cease, the airplane has positive stability; if they continue unevenly, the airplane has neutral stability; if they increase, the airplane is unstable.
Longitudinal stability is the quality that makes an airplane stable about its lateral axis. It involves the pitching motion as the airplane’s nose moves up and down in flight. Alongitudinally unstable airplane has a tendency to dive or climb progressively into a very steep dive or climb, or even a stall. Thus, an airplane with longitudinal instability becomes difficult and sometimes dangerous to fly.
Static longitudinal stability or instability in an airplane, is dependent upon three factors:
Location of the wing with respect to the center of gravity;
Location of the horizontal tail surfaces with respect to the center of gravity; and
The area or size of the tail surfaces.
In analyzing stability, it should be recalled that a body that is free to rotate will always turn about its center of gravity.
To obtain static longitudinal stability, the relation of the wing and tail moments must be such that, if the moments are initially balanced and the airplane is suddenly nosed up, the wing moments and tail moments will change so that the sum of their forces will provide an unbalanced but restoring moment which, in turn, will bring the nose down again. Similarly, if the airplane is nosed down, the resulting change in moments will bring the nose back up.
The center of lift, sometimes called the center of pressure, in most unsymmetrical airfoils has a tendency to change its fore and aft position with a change in the angle of attack. The center of pressure tends to move forward with an increase in angle of attack and to move aft with a decrease in angle of attack. This means that when the angle of attack of an airfoil is increased, the center of pressure (lift) by moving forward, tends to lift the leading edge of the wing still more. This tendency gives the wing an inherent quality of instability.
 Figure 3-12 shows an airplane in straight-and-level flight. The line CG-CL-T represents the airplane’s longitudinal axis from the center of gravity (CG) to a point T on the horizontal stabilizer. The center of lift (or center of pressure) is represented by the point CL.
Figure 3-12 shows an airplane in straight-and-level flight. The line CG-CL-T represents the airplane’s longitudinal axis from the center of gravity (CG) to a point T on the horizontal stabilizer. The center of lift (or center of pressure) is represented by the point CL.Most airplanes are designed so that the wing’s center of lift (CL) is to the rear of the center of gravity. This makes the airplane “nose heavy” and requires that there be a slight downward force on the horizontal stabilizer in order to balance the airplane and keep the nose from continually pitching downward. Compensation for this nose heaviness is provided by setting the horizontal stabilizer at a slight negative angle of attack. The downward force thus produced, holds the tail down, counterbalancing the “heavy” nose. It is as if the line CG-CL-T was a lever with an upward force at CL and two downward forces balancing each other, one a strong force at the CG point and the other, a much lesser force, at point T (downward air pressure on the stabilizer). Applying simple physics principles, it can be seen that if an iron bar were suspended at point CL with a heavy weight hanging on it at the CG, it would take some downward pressure at point T to keep the “lever” in balance.
 Even though the horizontal stabilizer may be level when the airplane is in level flight, there is a downwash of air from the wings. This downwash strikes the top of the stabilizer and produces a downward pressure, which at a certain speed will be just enough to balance the “lever.” The faster the airplane is flying, the greater this downwash and the greater the downward force on the horizontal stabilizer (except “T” tails). [Figure 3-13] In airplanes with fixed position horizontal stabilizers, the airplane manufacturer sets the stabilizer at an angle that will provide the best stability (or balance) during flight at the design cruising speed and power setting. [Figure 3-14]
Even though the horizontal stabilizer may be level when the airplane is in level flight, there is a downwash of air from the wings. This downwash strikes the top of the stabilizer and produces a downward pressure, which at a certain speed will be just enough to balance the “lever.” The faster the airplane is flying, the greater this downwash and the greater the downward force on the horizontal stabilizer (except “T” tails). [Figure 3-13] In airplanes with fixed position horizontal stabilizers, the airplane manufacturer sets the stabilizer at an angle that will provide the best stability (or balance) during flight at the design cruising speed and power setting. [Figure 3-14] If the airplane’s speed decreases, the speed of the airflow over the wing is decreased. As a result of this decreased flow of air over the wing, the downwash is reduced, causing a lesser downward force on the horizontal stabilizer. In turn, the characteristic nose heaviness is accentuated, causing the airplane’s nose to pitch down more. This places the airplane in a nose-low attitude, lessening the wing’s angle of attack and drag and allowing the airspeed to increase. As the airplane continues in the nose-low attitude and its speed increases, the downward force on the horizontal stabilizer is once again increased.
If the airplane’s speed decreases, the speed of the airflow over the wing is decreased. As a result of this decreased flow of air over the wing, the downwash is reduced, causing a lesser downward force on the horizontal stabilizer. In turn, the characteristic nose heaviness is accentuated, causing the airplane’s nose to pitch down more. This places the airplane in a nose-low attitude, lessening the wing’s angle of attack and drag and allowing the airspeed to increase. As the airplane continues in the nose-low attitude and its speed increases, the downward force on the horizontal stabilizer is once again increased.Consequently, the tail is again pushed downward and the nose rises into a climbing attitude.
As this climb continues, the airspeed again decreases, causing the downward force on the tail to decrease until the nose lowers once more. However, because the airplane is dynamically stable, the nose does not lower as far this time as it did before. The airplane will acquire enough speed in this more gradual dive to start it into another climb, but the climb is not so steep as the preceding one.
After several of these diminishing oscillations, in which the nose alternately rises and lowers, the airplane will finally settle down to a speed at which the downward force on the tail exactly counteracts the tendency of the airplane to dive. When this condition is attained, the airplane will once again be in balanced flight and will continue in stabilized flight as long as this attitude and airspeed are not changed.
A similar effect will be noted upon closing the throttle. The downwash of the wings is reduced and the force at T in figure 3-12 is not enough to hold the horizontal stabilizer down. It is as if the force at T on the lever were allowing the force of gravity to pull the nose down. This, of course, is a desirable characteristic because the airplane is inherently trying to regain airspeed and reestablish the proper balance.
 Power or thrust can also have a destabilizing effect in that an increase of power may tend to make the nose rise. The airplane designer can offset this by establishing a “high thrustline” wherein the line of thrust passes above the center of gravity. [Figures 3-15 and 3-16] In this case, as power or thrust is increased a moment is produced to counteract the down load on the tail. On the other hand, a very “low thrust line” would tend to add to the nose-up effect of the horizontal tail surface.
Power or thrust can also have a destabilizing effect in that an increase of power may tend to make the nose rise. The airplane designer can offset this by establishing a “high thrustline” wherein the line of thrust passes above the center of gravity. [Figures 3-15 and 3-16] In this case, as power or thrust is increased a moment is produced to counteract the down load on the tail. On the other hand, a very “low thrust line” would tend to add to the nose-up effect of the horizontal tail surface.It can be concluded, then, that with the center of gravity forward of the center of lift, and with an aerodynamic tail-down force, the result is that the airplane always tries to return to a safe flying attitude.
 Asimple demonstration of longitudinal stability may be made as follows: Trim the airplane for “hands off” control in level flight. Then momentarily give the controls a slight push to nose the airplane down. If, within a brief period, the nose rises to the original position and then stops, the airplane is statically stable. Ordinarily, the nose will pass the original position (that of level flight) and a series of slow pitching oscillations will follow. If the oscillations gradually cease, the airplane has positive stability; if they continue unevenly, the airplane has neutral stability; if they increase, the airplane is unstable.
Asimple demonstration of longitudinal stability may be made as follows: Trim the airplane for “hands off” control in level flight. Then momentarily give the controls a slight push to nose the airplane down. If, within a brief period, the nose rises to the original position and then stops, the airplane is statically stable. Ordinarily, the nose will pass the original position (that of level flight) and a series of slow pitching oscillations will follow. If the oscillations gradually cease, the airplane has positive stability; if they continue unevenly, the airplane has neutral stability; if they increase, the airplane is unstable.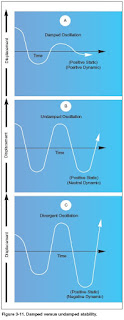


 Stability—The inherent quality of an airplane to correct for conditions that may disturb its equilibrium, and to return or to continue on the original flightpath. It is primarily an airplane design characteristic.
Stability—The inherent quality of an airplane to correct for conditions that may disturb its equilibrium, and to return or to continue on the original flightpath. It is primarily an airplane design characteristic.